Computational Complexity

Computational Complexity is a concept used in Computer Science to characterize the resources required for an algorithm to solve a certain problem.

The two resources Computer Scientists are most concerned about are:

• Time (how long does it take?)
• Space (how much storage does it need?)

It should be noted here that "time" gets translated to "number of operations" owing to its ease in comparison of other algorithms.

A Naive Approach

If we're comparing two algorithms we could try to just measure the duration of time and the amount of memory in terms of seconds and units of storage respectively.

The problem with this approach is that it's highly platform specific meaning you might get different running times/memory usage if you used a different machine. Furthermore, doing multiple runs might even give different times owing to the nature of Operating Systems, other processes, etc.

This proves to be rather problematic in comparing algorithm performance as there isn't any sense of a frame of reference for us.

Luckily, there is one property of algorithms that remains the same regardless of what machine it runs on: The growth of resource consumption relative to its input.

The growth itself has quantifiable properties that computer scientists like to focus on, such as the best-case, worst-case, and average-case scenarios.

The case that the majority are concerned with however, is the worst-case scenario. That is, given some input, what is the largest growth we can expect in terms of resource consumption?

Such a property is mathematically formalized as Big-O notation.

Big-O Notation

Big-O notation is a way of defining the upper-bound of an algorithms growth relative to its input or in plain English, the "worst case scenario".

The "growth" usually defaults to time complexity and therefore, number of operations unless there has been explicit statement that it is memory complexity that is being analyzed.

The exact definition is presented below:

\( f(n) = O(g(n)) \) if there exists a positive integer \( n_0 \) and a positive constant \( c \), such that \( f(n) \le c \cdot g(n) \hspace{0.5cm} \forall \hspace{0.1cm} n \ge n_0 \)

In plain English, a function \( f(n) \) can be considered "Big-O" of \( g(n) \) if you can find a number to plug into n such as (\( n_0 \)) and a constant \(c \) such that there is a point where \( c \cdot g(n) \) exceeds all values of \( f(n) \).

Let's try a quick example.

I have an algorithm who's resource consumption given some input data \( n \) grows by \( f(n) = 2n^2 + n + 5 \).

To find a suitable \(g(n)\) we just need to find some function that can, with some slight modification, outpace \(f(n)\)'s growth rate.

We could choose something like \(n!\) but the goal of Big-O is to find the best fitting bound , one that still fits the definition but bounds \(f(n)\) as close as possible from above.

With that in mind, \(10n^2\) can easily grow faster than the given \(f(n)\). To truly satisfy the definition, we need to find an exact \(n_0\). The constant \(10\) in front of the \(10n^2\) already satisfies the first requirement of having a positive constant multiplier \(c\).

We graph the two functions together and find our \(n_0\):

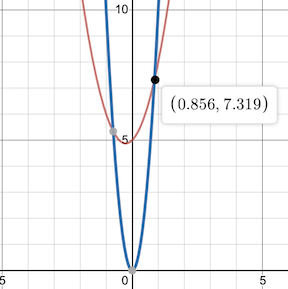
With the function found, as well as a suitable \(n_0\) and \(c\), we can now say the following

The function \(f(n)\) has Big-O of \(n^2\) time complexity.

With that understanding, the image below gives an idea for the different kinds of complexities you'll frequently bump into in the computer science world, as well as how to think of them qualitatively (is \(O(n)\) good or bad? What about \(O(log(n))\)?)

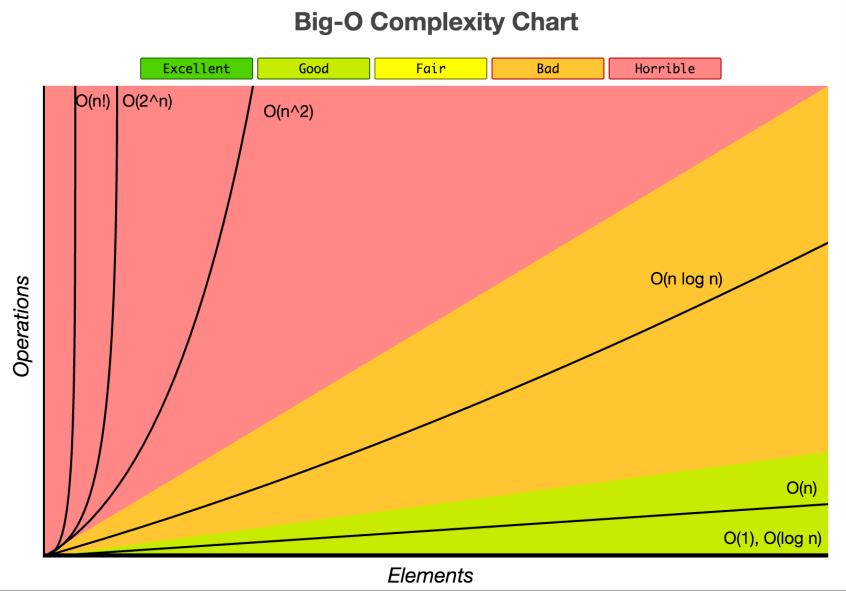
Source: Big-O Cheat Sheet

Tractability

Two words you might hear thrown around quite frequently (especially in Quantum Computing) is the idea of "tractability".

If an algorithm is intractable, its Big-O time complexity is greater than any polynomial or to be more formal, exceeds any variant of \(O(n^k)\) where \(k\) is some constant. The term superpolynomial is also equivalent.

If we look at the chart above, that would mean algorithms that have \(O(2^n)\) or \(O(n!)\) complexities are intractable.

In the opposite sense, if an algorithm is tractable it means its Big-O time complexity is less than or equal to that of any polynomial. The term subpolynomial is also equivalent.

If we go back to the chart, that would mean algorithms that have \(O(log(n))\), \(O(1)\), and \(O(n)\) time complexities can be considered to be tractable.

Complexity Classes

Complexity classes are a way of categorizing problems that take the same amount of resources to solve. You won't need to know what exactly the classes are for understanding the motivations behind Quantum Computing in the next section but it does help in understanding the degree of difficulty certain problems are considered to have as well as a more formal definition of the motivations you'll see soon.