Complexity Classes
Complexity classes are a way of categorizing problems based on the resources required to solve them.
This ties in nicely with Big-O and our definition of resource consumption based on the size of an algorithm's input.
The following Euler Diagram gives a nice graphical overview of the four most commonly encountered complexity-classes.
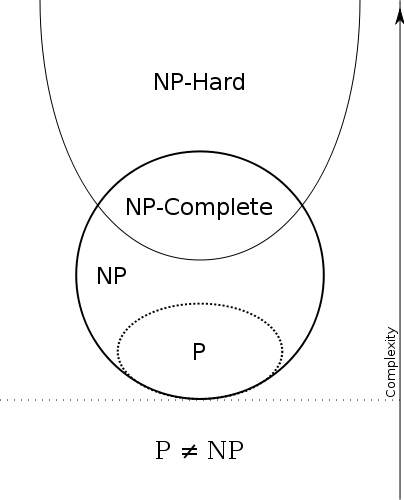
Source: Wikipedia Entry for NP-Completeness
Decision Problem
All the problems that the four categories above (P, NP, NP-Complete, NP-Hard) describe are known as Decision Problems.
A Decision Problem is any problem that has a yes or no answer. For Example:
- Given an integer, is it even or odd?
- Given a graph, does a Hamiltonian Cycle exist in it? (Given a bunch of points with lines between them, does a line exist that goes through each point exactly ONCE exist?)
P
P is the set of all decision problems that can be solved in polynomial time by a Deterministic TM (DTM), hence the letter "P" for "Polynomial time" 1
Recall that a DTM is a TM where each symbol on the tape corresponds to one and only one course of action.
Problems that fall into the P Complexity Class are:
- Identifying palindromes (Does a word remain the same if read from right to left as it is left to right?)
- Recognizing Substrings (given two strings a and b, can we find b in its entirety inside a?)
- Finding the Greatest Common Divisor of two numbers
NP
NP is the set of all decision problems that can be solved in polynomial time by a Non-Deterministic Turing Machine (NTM), hence "NP" for "Non-Deterministic Polynomial time". Alternatively, NP is the set of decision problems which can be verified in polynomial time by a DTM.2
Recall that an NTM is a TM where each symbol on the tape can correspond to a set of different actions each time an instruction is executed.
A problem that falls into NP is Integer Factorization where, given two numbers \(n\) and \(m\), does an integer \(f\) exist constrained by \(1 < f < m \) such that \(f\) divides \(n\)? Finding the solution will require some algorithm on an NTM but to actually verify if the solution is correct we just have to perform the division \(n / f \) which can be done in polynomial time by a DTM. 3
NP-Complete
NP-Complete is the set of problems that other problems in NP can be reduced to in polynomial time by a DTM.
This means if we can find an algorithm that can efficiently solve an NP-Complete problem, then other problems in NP can also be solved efficiently IF they can be reduced to the NP-Complete problem form.
A problem that falls into NP-Complete is the 3-SAT problem.
You're given a set of boolean variables arranged in the following configuration:
(X or Y or Z) AND
(B or D or F) AND
(J or K or L) AND
...
and you need to find the proper value for each boolean variable that will make the entire expression return "True".
It has been proven that every problem in NP is reducible to this problem. IF a polynomial time algorithm can be found to solve 3-SAT, it can solve every problem in NP efficiently. 4
NP-Hard
NP-Hard is the set of problems that are at least as hard as the NP-Complete problems. NP-Hard problems don't have to be in NP and they don't have to be decision problems either.
If you go back to the Euler Diagram, you'll find that it intersects with NP but also goes beyond it.
A more precise definition is that a problem \( X \) can be considered NP-Hard if there is an NP-Complete problem \( Y \) such that \(Y \) can be reduced to \(X \).
Since any NP-Complete problem can be reduced to any other NP-Complete problem in polynomial time, all NP-Complete problems can be reduced to any NP-Hard problem in polynomial time. Therefore, if you can find a solution to one NP-Hard problem in polynomial time, there is a solution to ALL NP problems in polynomial time.
A significant NP-Hard problem is the Halting Problem which states that given a program and its input, can you determine if the program will stop?. This is a decision problem but does not fall into NP. Any NP-Complete problem can be reduced to this one. 5
QC Complexity
In the realm of QC, there are analogues to the classes you've seen above. One of the yet unsolved questions in QC is where these classes lay with respect to other classes like P and NP. Finding this out is highly desirable because it could lead to the discovery of more problems that can be reduced or made faster on Quantum Computers that was once prohibitive to perform on classical computers.
There are two QC Complexity Classes you may encounter that are described here for the purpose of being thorough. Keep in mind that you do not need to know how a Quantum Computer works yet to understand these classes. The four classes above as well as the provided explanation should be enough for now.
BQP
BQP or Bounded-Error Quantum Polynomial Time (a mouthful), is a class of decision problems that is solvable by a Quantum Computer in polynomial time with an error probability of at most \( 1/3 \) for all instances. 6
It seems incredibly odd that we have to worry about "error" in our result but this comes from the nature of Quantum Computing, and Quantum Mechanics itself. In the quantum realm, the absolutes of our physical world give way to probabilities. The singular, absolute answers that Classical Computation gives are non-existent as Quantum Computers give answers in a kind of probability distribution.
This means that most quantum computing algorithms have to be run multiple times (similar to the Solovay-Strassen Test mentioned in the Church-Turing Thesis section) to obtain an accurate answer.
The classical analogue to BQP is BPP or Bounded-Error Probabilistic Polynomial Time which goes back to NTMs and the introduction of a probabilistic TM. In BPP, decision problems exist that are solvable in polynomial time with an error probability of at most, \( 1/3 \) by a probabilistic TM. BPP in turn, is the probabilistically bound relative of the more familiar P complexity class you should be familiar with which works with DTMs.7
Shor's Algorithm falls into the BQP Complexity class as well as some other notable problems such like the simulation of quantum systems and the Discrete Logarithm (to be explained in later sections, but of great importance to cryptographic systems).8
QMA
QMA or Quantum Merlin Arthur is class of decision problems for which a Quantum Computer can verify a solution in polynomial time. If this sounds familiar, it can be considered the quantum analogue of the NP class 9. It still has the error probability component you saw in BQP but it's a little more nuanced.
If the answer to the solution is YES, verification should be correct \( 2/3 \) of the time but if it is NO, verification should not say it is correct with an error of \( 1/3 \). There is some flexibility in these fractional bounds in that you can redefine them and the problem can still be considered to be in QMA but the accepted standard is \( 2/3 \) vs \( 1/3 \) 10
Citations
- Stack Overflow, What are the Differences Between NP, NP-Complete, and NP-Hard?
- Wikipedia Entry, NP (complexity)
- see 1.
- see 1.
- see 1.
- Wikipedia Entry, BQP
- Wikipedia Entry, BPP (complexity)
- see 6.
- CMU 18-859BB, Fall 2015 Lecture 24: Quantum Merlin-Arthur by Ryan O'Donnell & Sidhanth Mohanty
- Wikipedia Entry, QMA